抽空看了 Category Theory 有一種我到底看了什麼感覺

有點蛋疼 有點懂 有點不懂 有點有趣 有點WTF

反正整個五味雜成就是哩！

Category

首先，先提到 Category，以及事前準備(術語)

Category 到底有什麼東東

Category 會包含以下四個東東：

1. Objects
2. Morphisms 或稱 Arrows
3. Associative Law
4. Identity Law

在不同的面向來看這四個東東會對應到不同的東西。

已程式設計來說，可能會是下面的對應

1
2
3
4
5
6
7
8
9
10

func f(a:Int) -> Double {
    return Double(a + 1)
}

func g(b:Double) -> String {
    return String(b) + "2"
}

// function composition
g(f(1)) == (g ∘ f)(1)

1
2
3

func identity<T>(a:T) -> T {
    return a
}

1
2
3
4
5
6

public func ∘ <A,B,C> (f:(B -> C), g:(A -> B)) -> (A -> C) {
    func gof(a:A) -> C{
        return f(g(a))
    }
    return gof
}

Category 的 Laws

Category 必須遵循兩條 Lasw：

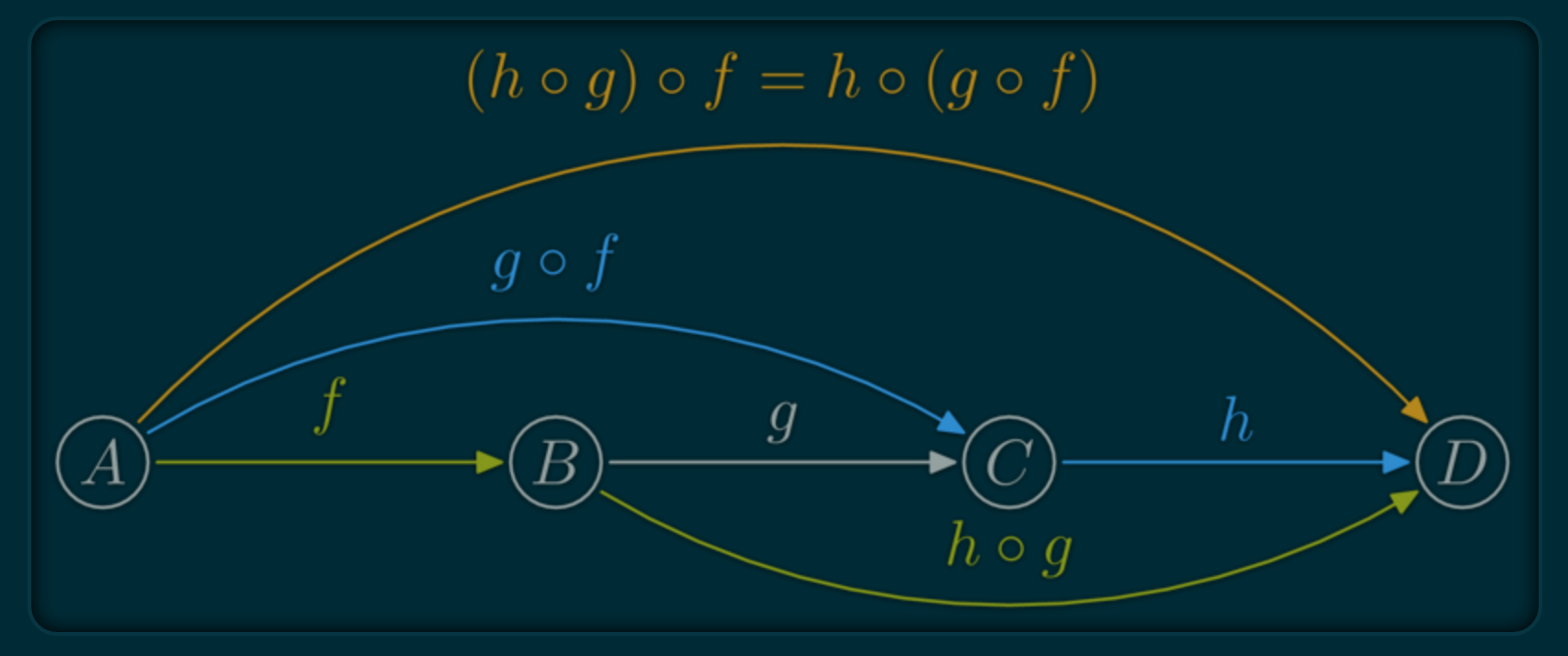
• Associative Law : (f ∘ g) ∘ h = f ∘ (g ∘ h)
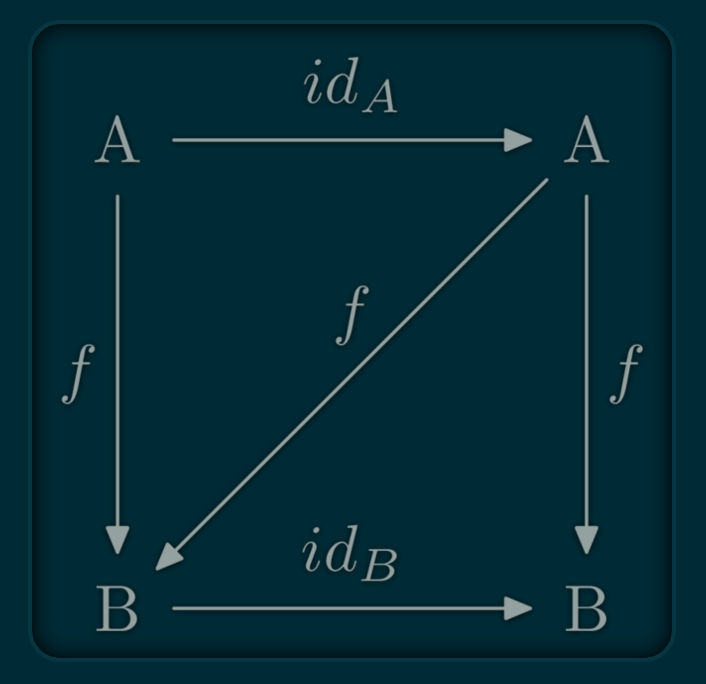
• Identity Law : f ∘ identity = f = identity ∘ f

某 function f g h:

1
2
3

f : A -> B
g : B -> C
h : C -> D

圖解定義

g(f(a)) = (g ∘ f)(a)

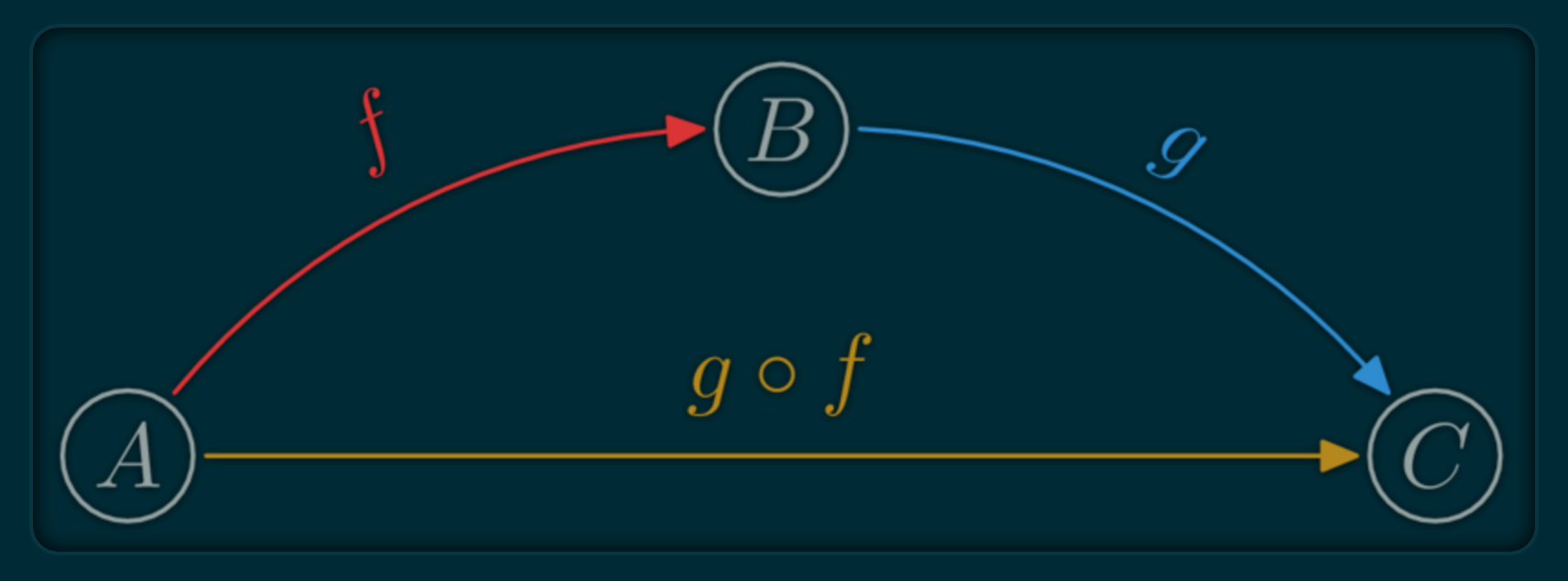
Associative Law

Identity Law

Functor

其實還是不懂，只好祭出 Haskell 定義

1
2

class Functor f where
    fmap :: (a -> b) -> f a -> f b

Monoid

不是很懂。但他有一條 tip 提到，具有 0 to many 特性幾乎就是Monoid。

一樣先提 Monoid 的事前準備(術語)

Compose function •:

1

• : M × M -> M

Identity function id:

1

id : M

同樣 Monoid 也必須遵循兩條規則：

• Associative Law : (f • g) • h = f • (g • h)
• Identity Law : f • id = f = id • f

以下是個人理解

例如 Int 可以找到 compose function(加法) 以及 id (0)
0 + x = x = x + 0

Int 可以找到 compose function(乘法) 以及 id (1)
1 x = x = x 1

String 可以找到 compose function(字串串接) 以及 id (“”)
“” + “a” = “a” = “a” + “”

椅子的話就不符合這個條件，椅子＋椅子 不等於 椅子

椅子堆反而可以
空椅子堆 ＋ 椅子堆 ＝ 椅子堆 ＝ 椅子堆 ＋ 空椅子堆

Reference

Category Theory & Programming
Category theory for beginners